[算法]堆排序

堆排序的主要步骤分为三部分:

1. 建堆
2. 维持堆的性质
3. 排序

首先是建堆,建堆的主要目的是建立一个最大堆,这样我们就可以保证堆顶的元素一定是这个数组中最大的元素.

void buildHeap(int *array, int size)
{
    for (int i = size / 2; i >= 0; i--)
    {
        maxHeapify(array, i, size);  //维持最大堆性质
    }
}

其次是维持最大堆性质,其过程如下:

1. 比较当前节点(父节点)和自己的2个子节点(可能是1个)的大小.
2. 将3个节点中最大值的点与当前节点交换位置.
3. 如果产生了节点交换,那么继续以交换后的节点作为父节点继续执行maxHeapify.
4. 直到不再产生节点位置交换.

void maxHeapify(int *array, int index, int size)
{
    int l = left(index);
    int r = right(index);
    int largest;
    if (l < size && array[l] > array[index])
    {
        largest = l;
    }
    else
    {
        largest = index;
    }

    if (r < size && array[r] > array[largest])
    {
        largest = r;
    }
    if (largest != index)
    {
        int temp = array[largest];
        array[largest] = array[index];
        array[index] = temp;
        maxHeapify(array, largest, size);
    }
}

最后则是排序过程,因为在建堆和维持堆持续后,已经产生了1个最大堆,那么剩下的过程只需要将数组的最后1位和根节点交换位置,将数组的length-1,然后继续维持堆的性质后,那么就又产生了1个最大堆,如此循环直到只剩下1个元素的时候.排序过程如下图:


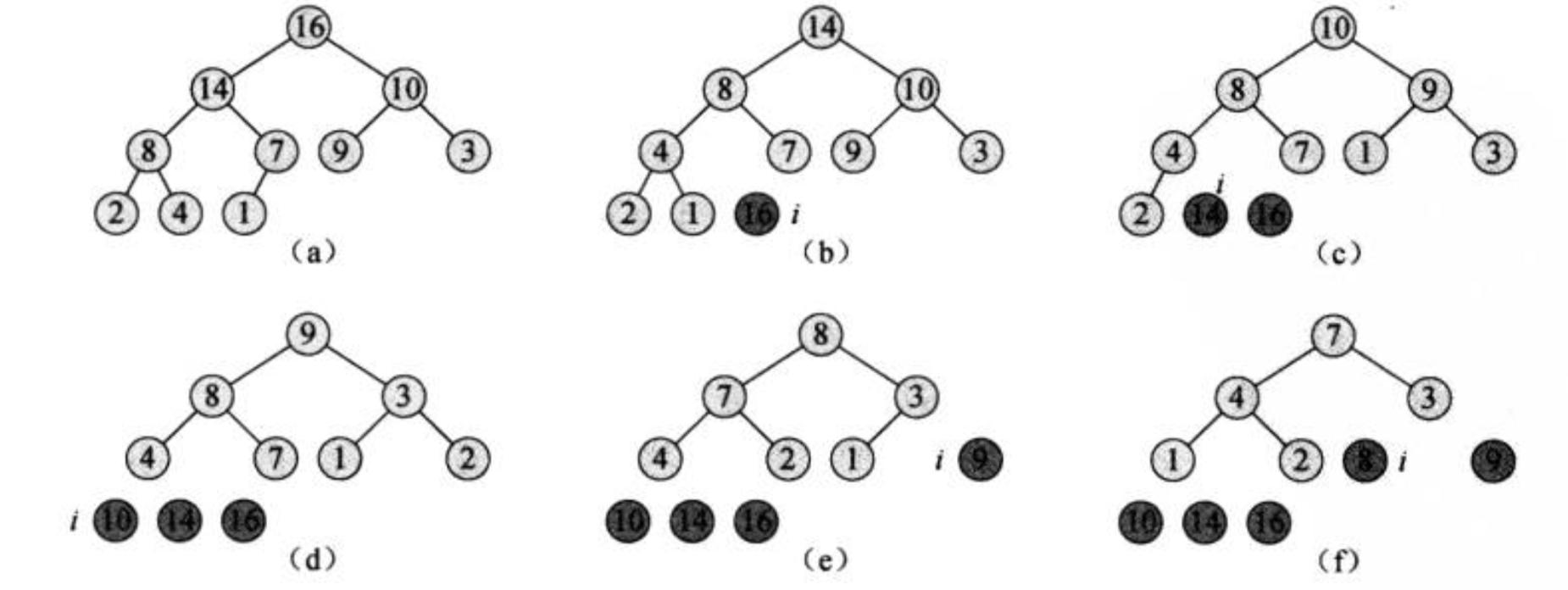
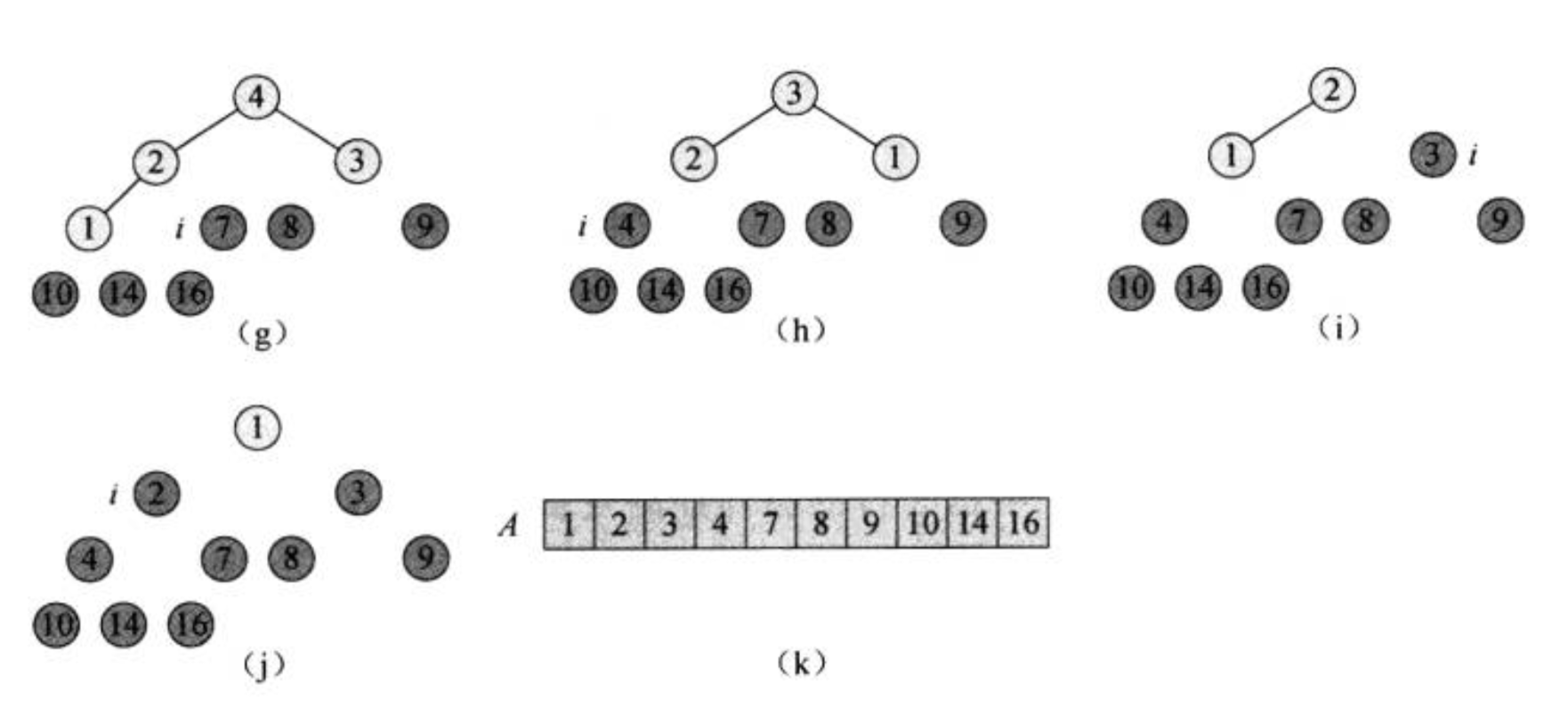
排序代码就很简单了,如下:

void heapSort(int *array, int size)
{
    buildHeap(array, size);
    int length = size;
    for (int i = length - 1; i >= 1; i--)
    {
        int temp = array[i];
        array[i] = array[0];
        array[0] = temp;
        size -= 1;
        maxHeapify(array, 0, size);
    }
}

最后附上完整代码

#include "iostream"
using namespace std;

int parent(int i)
{
    return i / 2;
}

int left(int i)
{
    return i * 2 + 1;
}

int right(int i)
{
    return i * 2 + 2;
}

void maxHeapify(int *array, int index, int size)
{
    int l = left(index);
    int r = right(index);
    int largest;
    if (l < size && array[l] > array[index])
    {
        largest = l;
    }
    else
    {
        largest = index;
    }

    if (r < size && array[r] > array[largest])
    {
        largest = r;
    }
    if (largest != index)
    {
        int temp = array[largest];
        array[largest] = array[index];
        array[index] = temp;
        maxHeapify(array, largest, size);
    }
}

void buildHeap(int *array, int size)
{
    for (int i = size / 2; i >= 0; i--)
    {
        maxHeapify(array, i, size);
    }
}

void heapSort(int *array, int size)
{
    buildHeap(array, size);
    int length = size;
    for (int i = length - 1; i >= 1; i--)
    {
        int temp = array[i];
        array[i] = array[0];
        array[0] = temp;
        size -= 1;
        maxHeapify(array, 0, size);
    }
}

int main()
{
    int array[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
    int size = sizeof(array) / sizeof(array[0]);
    heapSort(array, size);

    for (int i = 0; i < sizeof(array) / sizeof(array[0]); i++)
    {
        cout << array[i] << endl;
    }
    return 0;
}

堆排序的时间复杂度分析:

时间复杂度为O(nlgn).而且为原址排序算法(如果输入数组中仅有常数个数元素需要在排序过程存储在数据之外,则称排序算法是原址的).这里快速排序是原址的,但归并排序不是原址的,因为在合并过程中有额外的数组存储.

heapSort在建立初始最大堆后,它的时间复杂度为O(n),而length-1次的调用maxHeapify,每次调用时间复杂度为O(lgn).所以总时间复杂度位O(nlgn);